---

---

Writing Fractions

A fraction tells us how many parts of a whole we have.

Here we have part of a shape shaded red.

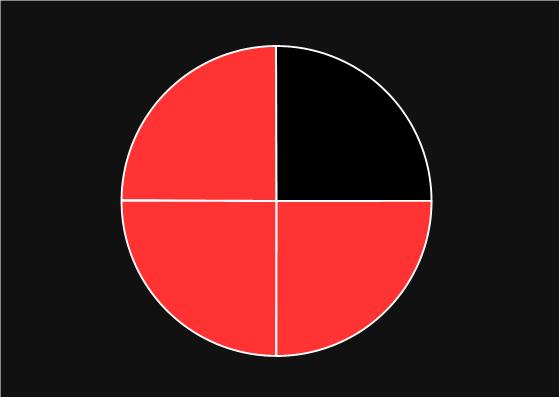
To write the fraction of the shape that is shaded red we need to count how many parts of the shape there are in total, there are 4 parts.

Then we count how many parts are shaded in red, 3 are red.
So we can say that 3 out of 4 are red.

To write this as a fraction we put the 3 on top, then a line, and then the 4.

The number on the top is called the numerator and the number on the bottom is called the denominator.

---

Try these:

---

Equivalent Fractions

Here we have part of a shape shaded red. We have 1 part out of 2, shaded red.

1⁄2  of the shape is shaded.

Here we have the same shape cut into 4 pieces, this time 2 parts out of 4 are shaded red.

2⁄4  of the shape is shaded.

Here we have the same shape cut into 6 pieces, this time 3 parts out of 6 are shaded red.

3⁄6  of the shape is shaded.

In each of theses shapes the same amount of the shape is shaded

1⁄2 ,   2⁄4  and  3⁄6  are equivalent fractions.

They all represent the same amount of a whole.

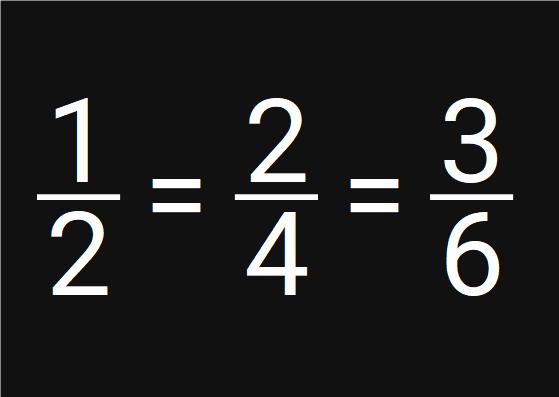
If you multiply the top (the numerator) and the bottom (the denominator) by the same number you get an equivalent fraction.

---

Example 1:  Write down 5 fractions equivalent to 2⁄3

We can multiply the numerator and the denominator by 2:
2 × 2 = 4
3 × 2 = 6
2⁄3 = 4⁄6

We can also multiply the numerator and the denominator by 3:
2 × 3 = 6
3 × 3 = 9
2⁄3 = 6⁄9

We can also multiply the numerator and the denominator by 4:
2 × 4 = 8
3 × 4 = 12
2⁄3 = 8⁄12

We can also multiply the numerator and the denominator by 5:
2 × 5 = 10
3 × 5 = 15
2⁄3 = 10⁄15

We can also multiply the numerator and the denominator by 6:
2 × 6 = 12
3 × 6 = 18
2⁄3 = 12⁄18

We could keep going with this list, writing down equivalent fractions forever. There will be an infinite number of fractions equivalent to 2⁄3

---

Try these:

---

Simplifying Fractions

Example 2:  Simplify  12⁄20

To simplify a fraction we need to get the smallest possible numbers for the numerator and denominator.

We need to find the biggest times table that the numerator and denominator are both in.
12 and 20 are both in the 4 times table.
12 = 4 × 3
20 = 4 × 5

Therefore, we can say that  12⁄20 = 3⁄5

3⁄5 and 12⁄20 are equivalent fractions.

3 and 5 are not in the same times table (apart from the 1 times table) so we cannot simplify it any more.

The answer is  3⁄5

---

Try these:

---

Ordering Fractions

To order fractions we can either convert them all to decimals or we can make all of the denominators the same using equivalent fractions.

Example 3: Put these fractions in order of size, start with the smallest fraction:

3⁄5  7⁄10  13⁄20  3⁄4

We are going to make the denominators the same for all of the fractions.
We need a number that is in the 5, 10, 20 and 4 times tables

20 is the lowest number in all the (4, 5, 10 and 20) times tables. We can make all of the denominators 20 using equivalent fractions.

Multiplying top and bottom by 4:  3⁄5  =   12⁄20

Multiplying top and bottom by 2:  7⁄10  =   14⁄20

Multiplying top and bottom by 5:  3⁄4  =   15⁄20

We also have  13⁄20

We can now order the fractions.

12⁄20  13⁄20  14⁄20  15⁄20

3⁄5  13⁄20  7⁄10  3⁄4

---