Transformations
There are 4 types of transformations we need to know:
• Translations
• Rotations
• Reflections
• Enlargements
Translations
A translation moves a shape. All points of the shape must be moved by the same amount.
A translation can be up or down and left or right.
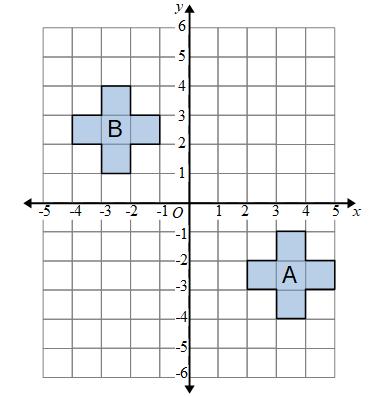
Example: Describe the transformation that maps shape A onto shape B
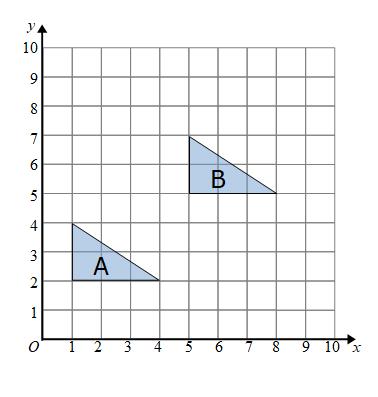
We can see that the shape has moved and all points have moved by the same amount. This transformation is called a translation
We also need to know by how much the shape has moved.
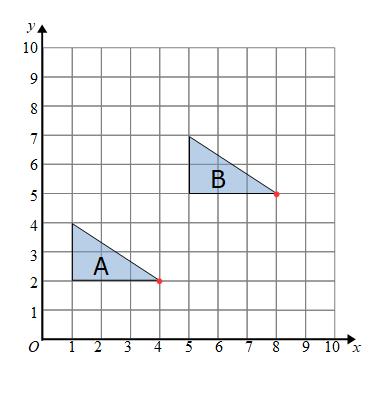
We can take any point of shape A and see how far we have to move to get to the same point on shape B.
We need to know how far to move left/right and how far to move up/down.
If we take the bottom right corner of A we have to see how far we have to move the to get to the bottom right corner of B.
We start by looking at how far to move left or right. We need to move 4 to the right.
Now we can look at how far up or down to move. We need to go up 3.
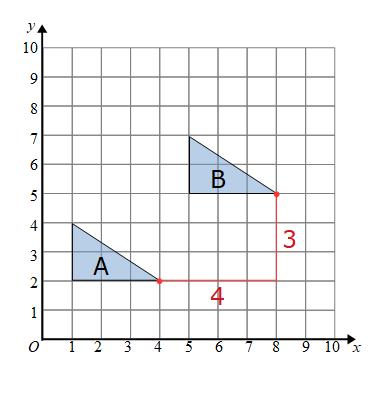
The transformation that maps shape A onto shape B is a translation 4 right and 3 up.
We can describe a translation using a vector.
4 right and 3 up can be written as:
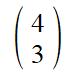
We write the left/right movement on top of the up/down movement. We put a set of brackets around these numbers.
A movement to the right is positive and a movement to the left is negative.
A movement up is positive and a movement down is negative.
5 left and 1 up is written as:
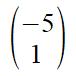
6 right and 2 down is written as:
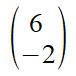
3 left and 8 down is written as:
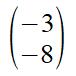
Example: Describe the transformation that maps shape A onto shape B
We have a translation.
To find out how much the shape has moved we need to pick a point on shape A and find the same point on shape B.
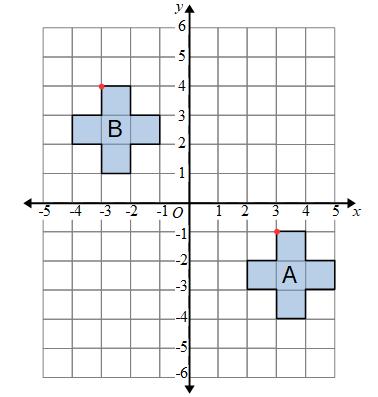
We can now look at how far we need to move to get from the point on A to the same point on B
Firstly we look at the left or right direction:
We need to move 6 to the left.
Next we look at how far to move in the up or down direction:
We move 5 up.
We have a translation 6 to the left and 5 up.
We can write 6 left and 5 up as a vector:
The transformation is a translation by the vector 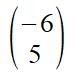
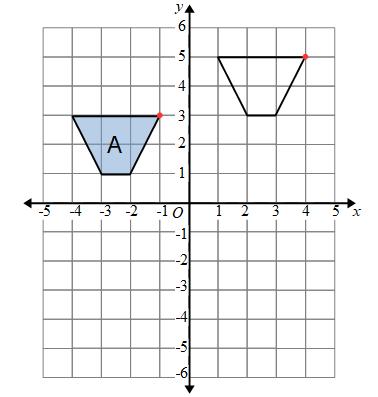
Example: Translate shape A by the vector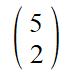
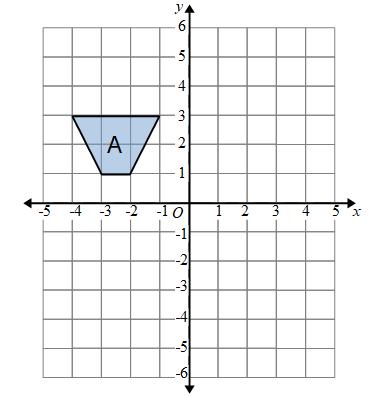
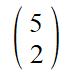 means we need to move the shape 5 right and 2 up
means we need to move the shape 5 right and 2 up
We can start by picking a point on shape A.
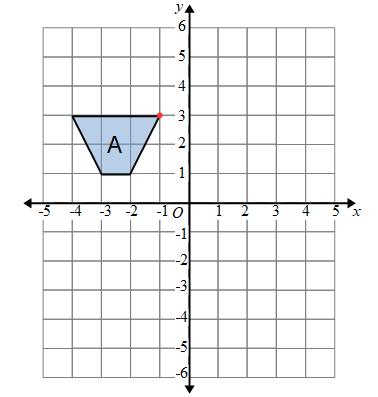
We can now move this point 5 right and then 2 up.
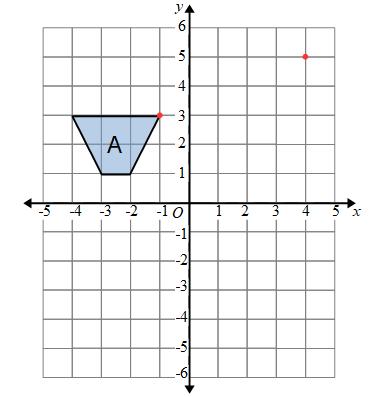
From this point we need to draw a shape that is the same as shape A.
Rotations
A rotation turns a shape around a fixed point. The fixed point is called the centre of rotation.
Example: Rotate shape A 180° about centre (1,1)
We can use tracing paper to rotate a shape
On the tracing paper we draw around the shape and mark the centre of rotation
We can also add an arrow pointing up from the centre of rotation
We now need to hold the tracing paper at the centre of rotation (you can hold a pencil on the centre of rotation) and spin the tracing paper around 180°
When the tracing paper has spun 180° the arrow will be facing down
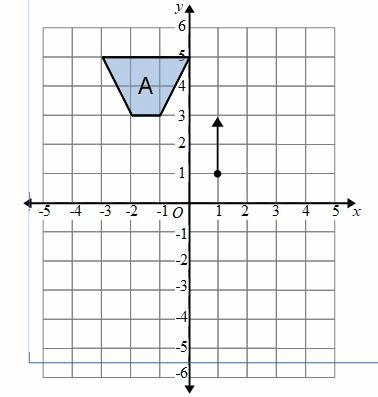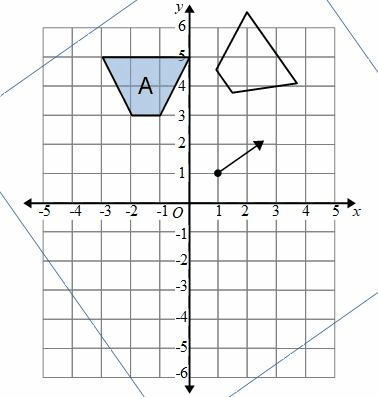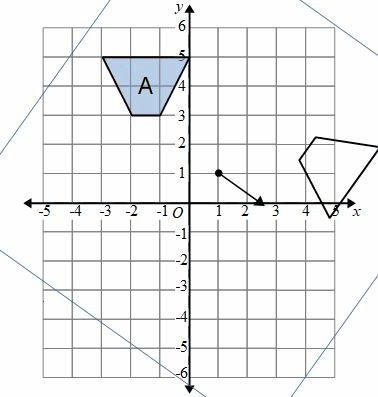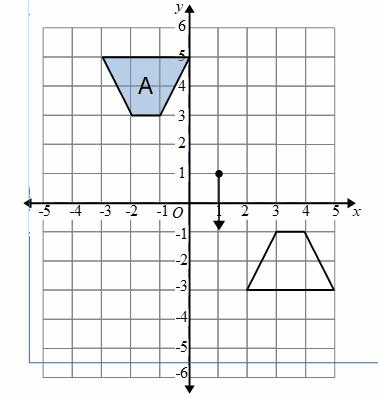
To finish we need to draw the rotated shape on the paper
Example: Describe the transformation that maps shape A onto shape B.
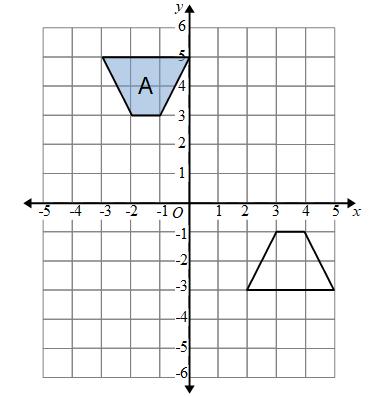
Here the shape has been turned, we have a rotation.
To describe the transformation we also need to know the centre of rotation and how far the shape has turned (the angle)
We can use tracing paper to help work this out.
To do this we get a piece of tracing paper and draw around the shape (shape A).
We then have to work out where to hold the tracing paper (the bit of the paper that is kept in the same position when the paper is rotated).
You can try different positions
If the tracing paper is held at (3,2) shape A should spin onto shape B.
(3,2) is the centre of rotation
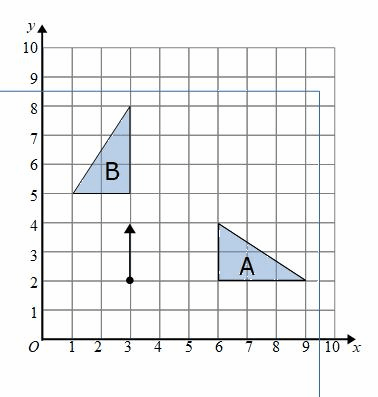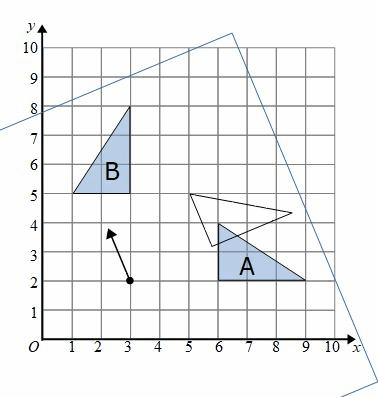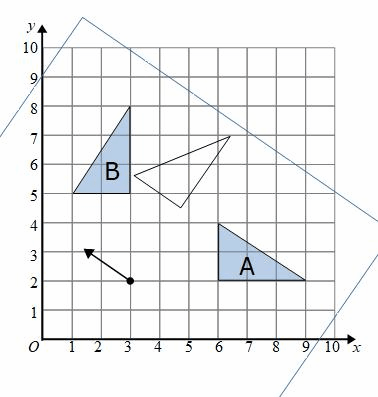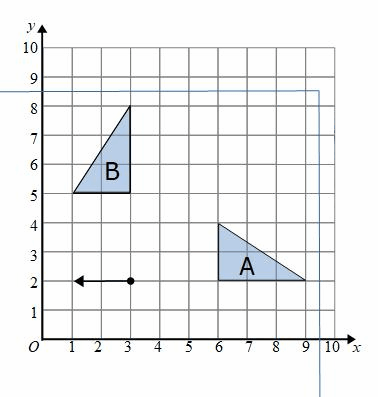
At (3,2) on the tracing paper we can draw an arrow facing up
If we hold the tracing paper at (3,2) and rotate the paper we will see that the arrow is facing left when the triangle is on shape B.
This is a 90° anticlockwise rotation.
We have a rotation, 90° anticlockwise, about the centre (3,2)
Reflections
A reflection is a mirror image of a shape. For a reflection we need a line of reflection (a mirror line). When a shape is reflected it is flipped over the mirror line.
After a shape is reflected each new point is the same distance from the mirror line as the original point.
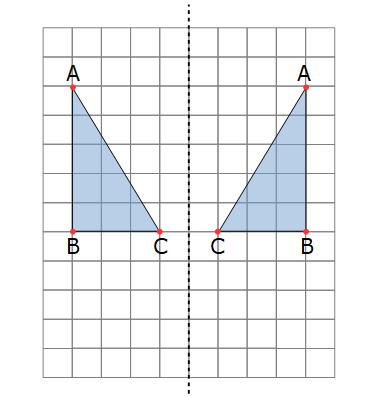
Here we have a shape reflected over a mirror line. The mirror line is shown by the dotted line.
You can see that each point and its corresponding point on the reflected shape are the same distance away from the mirror line.
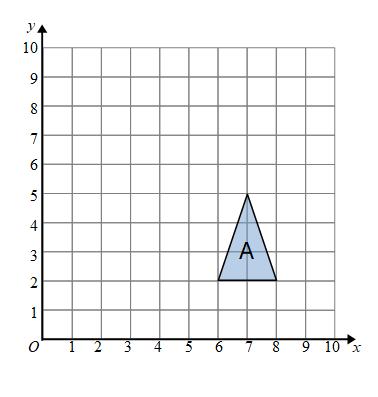
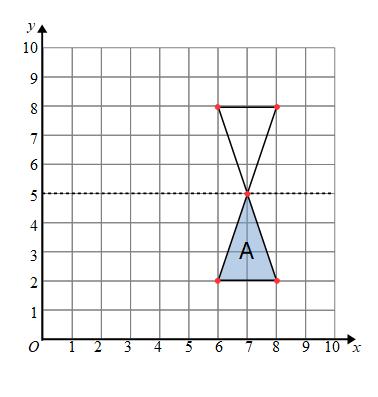
Example: Reflect shape A in the line y = 5
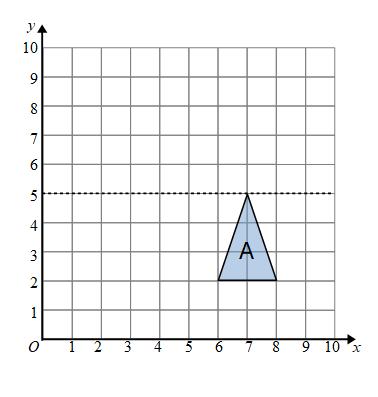
The line y = 5 is the line that joins all the points where y is 5. We can draw the mirror line with a dotted line.
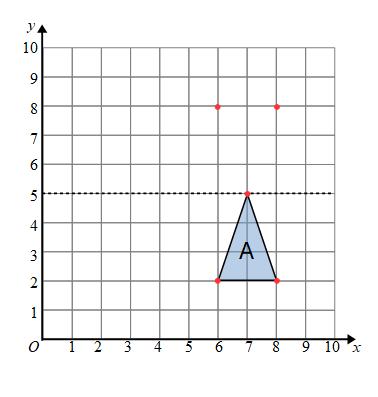
One corner of the triangle (7,5) is on the mirror line. This point will stay in the same position.
The corner at (6,2) is 3 units away from the mirror line (we always look at the shortest distance/perpendicular distance), it will be 3 units away on the other side of the mirror line.
The corner at (8,2) is 3 units away from the mirror line. It will be 3 units away on the other side of the mirror line.
Finally we connect the points to draw the reflected shape.
Example: Describe the single transformation that maps shape A onto shape B.
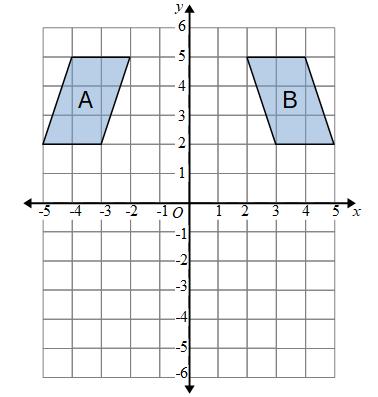
We can see that the shape has been flipped, we have a reflection.
We also need to know the mirror line.
The mirror line is half way between each set of corresponding points.
The mirror line is the y axis.
The transformation is a reflection in the y axis
The mirror line is not always a horizontal or vertical line.
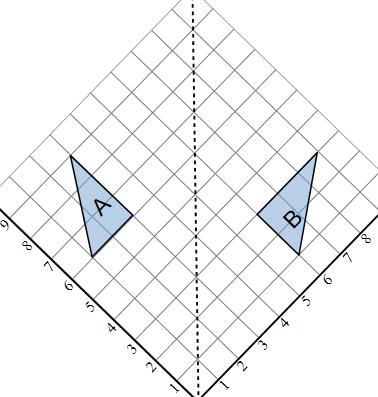
Here is another reflection.
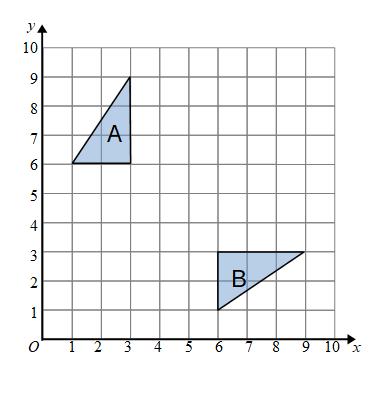
The mirror line is in the diagonal line that goes through (0,0), (1,1), (2,2), (3,3) and so on.
This line is called y = x
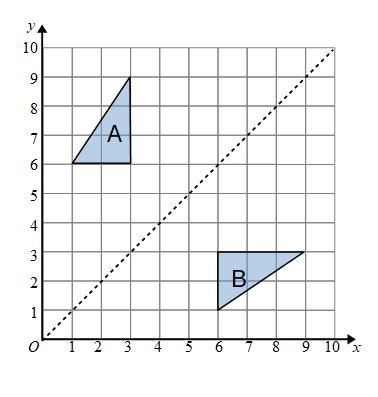
It can be easier to see if you rotate the page
Enlargements
An enlargement changes the size of a shape. The shape can get bigger or smaller.
To enlarge a shape we need to know the scale factor and the centre of enlargement.
The scale factor tells us how many times bigger (or smaller) the shape is.
The centre of enlargement is the starting point, the point from which the enlarged.
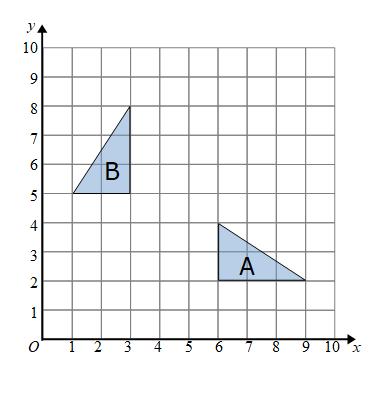
Example: Describe the transformation that maps shape A onto shape B.
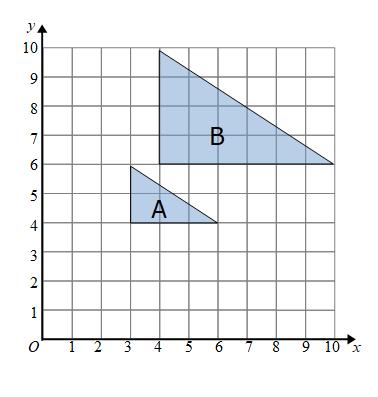
We can see that the shape has changed size. It is an enlargement.
Triangle A has base of 3 units and triangle B has a base of 6 units
Triangle A has a height of 2 units and triangle B has a height of 4 units
The scale factor is 2. (3 × 2 = 6 and 2 × 2 = 4)
To find the centre of enlargement we can extend a line through each set of corresponding points:
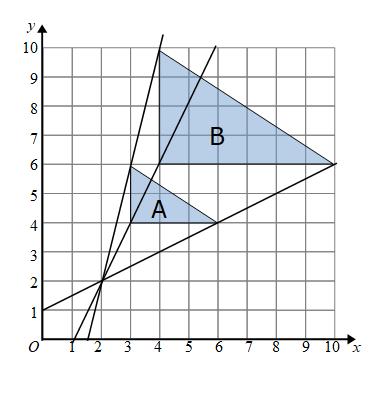
We can see that all of the lines meet at (2,2). This is the centre of enlargement.
The points on B are twice as far as their corresponding points on A from (2,2).
The transformation is an enlargement, scale factor 2 with centre of enlargement (2,2)
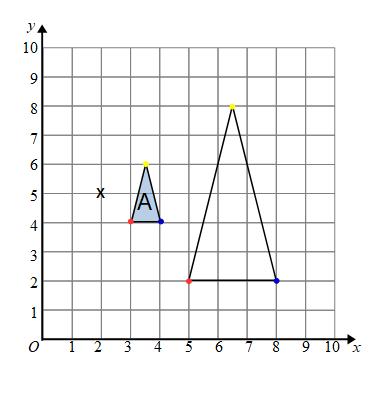
Example: Enlarge shape A by scale factor 3, centre (2,5).
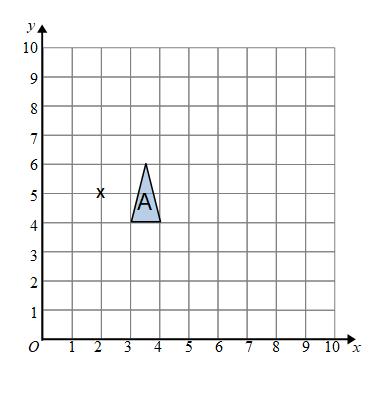
The centre of enlargement is marked with a cross (x).
All the points on the new shape will be 3 times as far from the centre of enlargement as their corresponding points on A.
To get from the centre of enlargement to the bottom left corner (the red point) of A we have to go along one and down one.
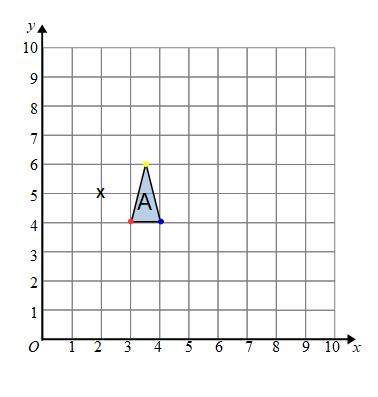
The corresponding point on the new shape will be 3 times as far. To get there we go along 3 and down 3 (from the centre of enlargement).
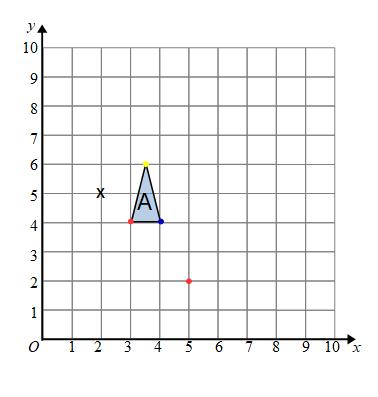
To get from the centre of enlargement to the bottom right corner (the blue dot) we have to go along 2 and down 1. The point on the new shape will be 3 times as far, it will be along 6 and down 3 from the centre of enlargement.
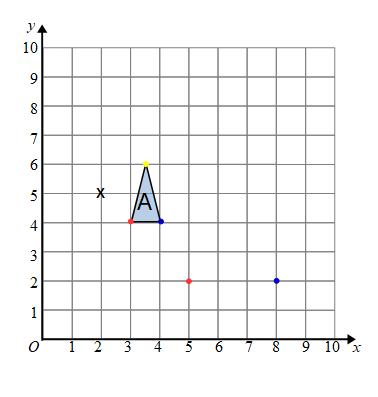
To get from the centre of enlargement to the top of the triangle (yellow dot) we have to go along 1.5 and up 1. We multiply by 3 for the enlarged shape. The new point will be along 4.5 and up 3 from the centre of enlargement.
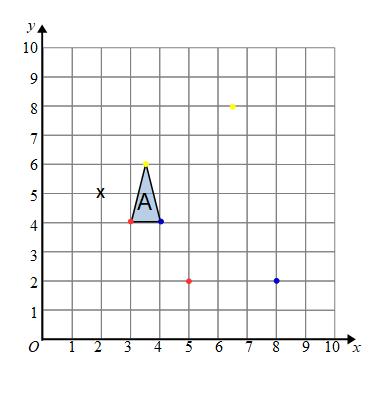
We can now connect the corners to form our transformed shape.
Example: Describe the single transformation that maps shape A onto shape B.
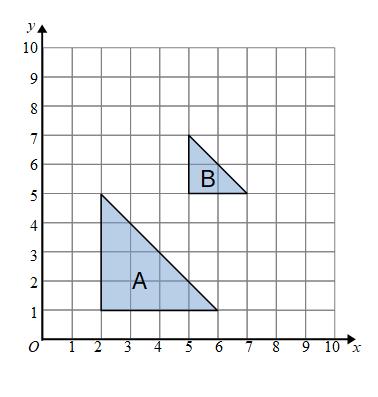
We can see that shape B is smaller than shape A. This is an Enlargement. (Any change in the size of the shape is called an enlargement.)
Shape A has a base of 4 units and shape B has a base of 2 units. 2 is half of 4. The scale factor is 0.5. The lengths of shape B are half the lengths of shape A.
To find the centre of enlargement we can extend lines through each corner and the corresponding corner on the other shape.
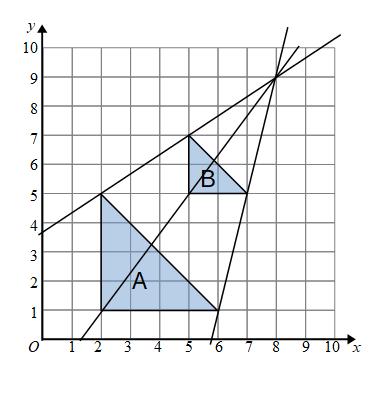
All the lines meet at (8,9). (8,9) is the centre of enlargement.
The transformation is an enlargement, scale factor 0.5, centre (8,9)