---

Example 1: Abbie and Ben share £120 in the ratio 2:1
Work out how much each of them get.

The first step is to work out how many equal parts there are.
The ratio is 2:1 so there are 3 (2 + 1) equal parts

We now need to work out how much each of the parts is worth
We divide the £120 between the 3 parts
£120 ÷ 3 = £40
Each part is worth £40

Now we can work out how much Abbie and Ben get
Abbie has 2 parts so she gets £80 (2 × £40)
Ben has one part which is worth £40

---

You may find it useful to draw a diagram for ratio questions

Abbie has 2 parts and Ben has 1 part, we could represent this as 2 boxes for Abbie and 1 box for Ben:

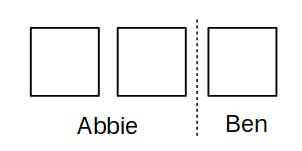
Each box must have the same amount in it and the total in all 3 boxes must be £120. We share £120 out evenly between the boxes (£120 ÷ 3 = £40)

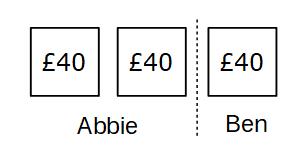
We can see that Abbie gets £80 (£40 + £40) and Ben gets £40

---

Example 2: A, B and C share £240 in the ratio 4:3:1
Work out how much each of them get.

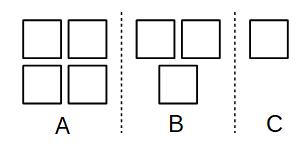
4 + 3 + 1 = 8
There are 8 equal parts

£240 ÷ 8 = £30
Each part is worth £30

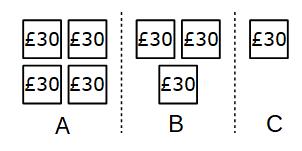
A gets 4 × £30 = £120
B gets 3 × £30 = £90
C gets 1 × £30 = £30

---

Try these:

---

Example 3: A and B share some money in the ratio 5:2
A gets £40
Work out how much B gets.

In this example we have not been given the total amount. We have been given the amount that A gets

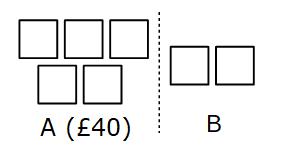
A has £40 and that is 5 parts

Each part much be equal so each part is worth £40 ÷ 5
£40 ÷ 5 = £8

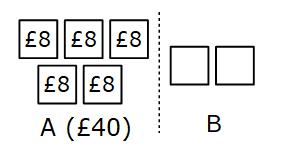
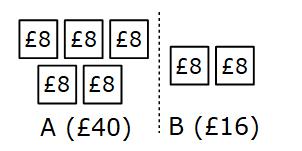
Each part is worth £8 and B has two parts
£8 × 2 = £16

---

Example 4: C and D share some money in the ratio 3:5
The difference between the amount C gets and the amount D gets is £18
Work out how much each of them get.

In this example we have been given the difference between the amounts of money C and D get.

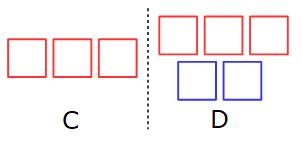
The difference between 3 parts and 5 parts is 2 parts. (5 − 3 = 2)
2 parts must be worth £18
£18 ÷ 2 = £9

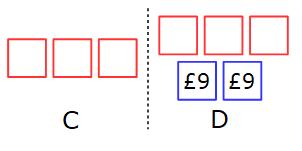
Each part is worth £9

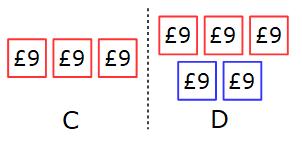
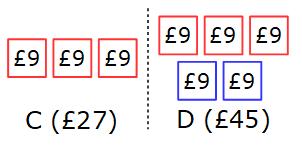
C gets 3 × £9 = £27
D gets 5 × £9 = £45

---

Try these: