Probability describes how likely something is to happen, it can be written as a fraction, a decimal or as a percentage.
Writing Probability and The Probability Scale
The probability scale runs from 0 to 1
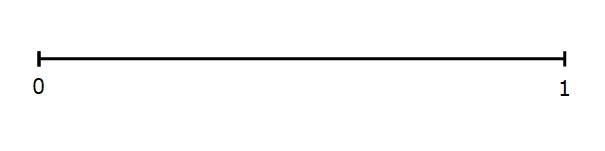
0 represents something that is impossible
If something has a probability of 1 it is certain to happen
Here we have a fair spinner. (We say the spinner is fair if the chance of landing on each side is equal.)
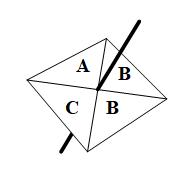
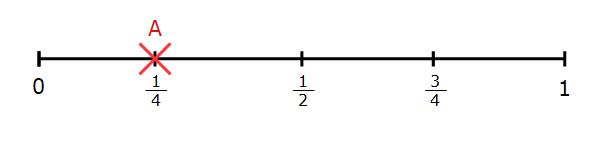
There are 4 sides, one of the sides has an A on it. We can say the probability of the spinner landing on A is
If we mark this on the probability scale, it will be
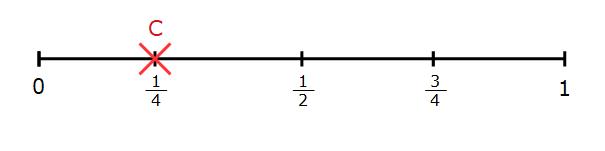
The probability of the spinner landing on C is also
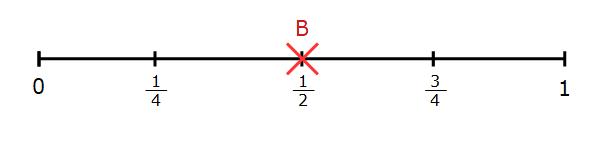
2 of the 4 sides have a B on. We can say the probability of the spinner landing on B is
If we mark this on the probability scale, it will be
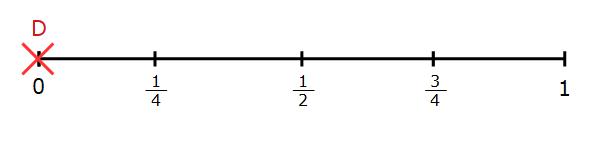
The probability of getting any letter other than A, B or C is 0. It would be impossible for the spinner to land on D. We can mark D on the probability scale at 0.
Example 1: In a bag there are 5 red counters, 4 blue counters and 3 yellow counters
A counter is picked at random find the probability that the counter will be
a) Red
b) Blue
c) Yellow
The total number of counters in the bag = 5 + 4 + 3 = 12
a) 5 out of 12 counters are red
the probability of picking a red counter will be
b) 4 out of 12 counters are blue, the probability of picking a blue counter will be
c) 3 out of 12 counters are yellow, the probability of picking a yellow counter will be
Because the counter can only be red or blue or yellow the three probabilities must add up to 1
The probabilities of all possible events will always add to 1 (or 100%)
Example 2: The probability of it raining tomorrow is 60%. Work out the probability of it not raining tomorrow.
The probability of it raining and the probability of it not raining must add up to 1 (or 100%)
100% - 60% = 40%
The probability of it not raining = 40%
Example 3: The probability of Roger winning a tennis match is
The probability of Roger winning and the probability of Roger not winning must add up to 1
1 -
The probability of Roger not winning =
Example 4: There are 20 pens in a box.
8 of the pens are black
3 of the pens are green.
The rest of the pens are red.
One of the pens is chosen at random
Find the probability that the pen is red.
We can work out how many red pens there are by calculating
20 - 8 - 3
20 - 8 - 3 = 9
There are 9 red pens and there are 20 pens in total
The probability of getting a red pen =
Try these: